Acerca de Discontinuidad de una función

El estudio de la discontinuidad de funciones es muy útil para sacar los puntos o los tramos de una función en los que es continua o discontinua.

Una función f es discontinua en a (o tiene una discontinuidad en a) si se cumplen al menos una de estas tres condiciones:

1. No existe la función en a, es decir, no existe la imagen de a:

   

2. No existe el límite de f en el punto x = a:

   

3. La imagen de a y el límite de la función en a son diferentes.
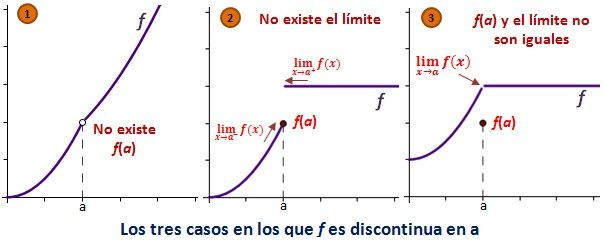
4. Cuando una función es discontinua en un punto, se pueden producir tres tipos de discontinuidades:
   • Discontinuidad evitable
   • Discontinuidad inevitable
   • Discontinuidad esencial

5. Discontinuidad evitable

   Una función f tiene una discontinuidad evitable en a si se cumplen las dos condiciones siguientes:

   

   • Existe el límite en a y éste es finito.

     

     • La imagen de a no existe o si existe no coincide con su límite.

       

   • Se dice que la discontinuidad es evitable porque se podría evitar definiendo la imagen de a como el valor de su límite en este punto.

     Ver ejemplo de discontinuidad evitable

     Discontinuidad inevitable

     Una función f tiene una discontinuidad inevitable en a si los límites laterales existen pero no coinciden, es decir:

     

     

     Se dice que la discontinuidad es inevitable porque no existe ninguna forma de juntar los dos laterales en a al ser distintos.

     Definiremos como el salto a la diferencia en valor absoluto de los límites laterales.

     

     Según si el salto es finito o infinito se clasifica la discontinuidad inevitable en:

     • Discontinuidad inevitable de salto finito

       El salto que se produce entre límites laterales es un número real finito. También se llama discontinuidad inevitable finita.

       

       

     • Discontinuidad inevitable de salto infinito

       El salto que se produce entre límites laterales es infinito.

       

       

       En este caso, también se llama discontinuidad inevitable infinita.
       Discontinuidad esencial
       Una función f tiene una discontinuidad esencial en a si no existe un límite lateral o no existen ambos:
       
       
       Por ejemplo, en el gráfico que tenemos arriba, la función tiene una discontinuidad esencial en , al no tener límite lateral por la izquierda en x=1.