Aprende un poco más
Cuando una ecuación lineal está graficada en un plano cartesiano, la recta divide el plano en dos partes. Cada parte es llamada medio plano. El diagrama a continuación muestra cómo los medios planos son formados cuando graficamos una ecuación lineal.
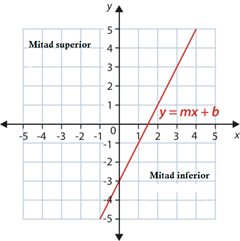 También se puede graficar una inecuación lineal en dos variables. En vez de solo graficar la recta límite (y=mx+b), también debes incluir todos los otros pares ordenados que podrían ser soluciones para la inecuación. Esto se llama conjunto solución y se muestra sombreando o coloreando el medio plano que incluye las soluciones adecuadas.
También se puede graficar una inecuación lineal en dos variables. En vez de solo graficar la recta límite (y=mx+b), también debes incluir todos los otros pares ordenados que podrían ser soluciones para la inecuación. Esto se llama conjunto solución y se muestra sombreando o coloreando el medio plano que incluye las soluciones adecuadas.
Cuando graficamos inecuaciones en dos variables necesitamos recordar cuando el valor está incluido (≤ o ≥) o no incluido ( o ). Para representar estas inecuaciones en un plano cartesiano en vez de círculos sombreados usamos líneas punteadas. Podemos decir qué mitad del plano pertenece a la solución mirando el signo de inecuación.
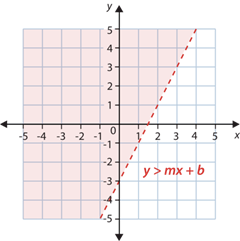 La solución de y≥mx+b es el medio plano sobre la recta y todos los puntos en la recta.
La solución de y≥mx+b es el medio plano sobre la recta y todos los puntos en la recta.
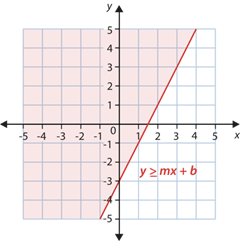 La solución de es el medio plano bajo la recta.
La solución de es el medio plano bajo la recta.
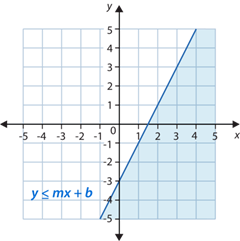
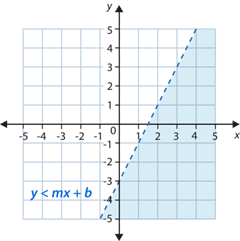 La solución de y≤mx+b es el medio plano bajo la recta y todos los puntos en la recta.
La solución de y≤mx+b es el medio plano bajo la recta y todos los puntos en la recta.
 Ejemplo A
Ejemplo A
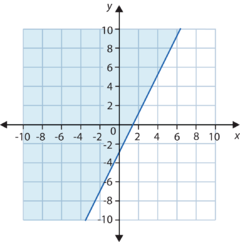
Grafica la inecuación y≥2x−3.
Solución:
Esta inecuación está en forma pendiente-intercepto. Comienza por graficar la recta. Luego determina qué medio plano se debe colorear.
 También se puede graficar una inecuación lineal en dos variables. En vez de solo graficar la recta límite (y=mx+b), también debes incluir todos los otros pares ordenados que podrían ser soluciones para la inecuación. Esto se llama conjunto solución y se muestra sombreando o coloreando el medio plano que incluye las soluciones adecuadas.
También se puede graficar una inecuación lineal en dos variables. En vez de solo graficar la recta límite (y=mx+b), también debes incluir todos los otros pares ordenados que podrían ser soluciones para la inecuación. Esto se llama conjunto solución y se muestra sombreando o coloreando el medio plano que incluye las soluciones adecuadas.Cuando graficamos inecuaciones en dos variables necesitamos recordar cuando el valor está incluido (≤ o ≥) o no incluido ( o ). Para representar estas inecuaciones en un plano cartesiano en vez de círculos sombreados usamos líneas punteadas. Podemos decir qué mitad del plano pertenece a la solución mirando el signo de inecuación.
- La solución es el medio plano sobre la recta.
- ≥ La solución es el medio plano sobre la recta y también todos los puntos en la recta.
- La solución es el medio plano bajo la recta.
- ≤ La solución es el medio plano bajo la recta y también todos los puntos en la recta.
 La solución de y≥mx+b es el medio plano sobre la recta y todos los puntos en la recta.
La solución de y≥mx+b es el medio plano sobre la recta y todos los puntos en la recta. La solución de es el medio plano bajo la recta.
La solución de es el medio plano bajo la recta. La solución de y≤mx+b es el medio plano bajo la recta y todos los puntos en la recta.
La solución de y≤mx+b es el medio plano bajo la recta y todos los puntos en la recta. Ejemplo A
Ejemplo AGrafica la inecuación y≥2x−3.
Solución:
Esta inecuación está en forma pendiente-intercepto. Comienza por graficar la recta. Luego determina qué medio plano se debe colorear.
- La inecuación es ≥, por lo tanto la recta es sólida.

